This article explores how to simulate bond yields and equity prices, providing a foundational understanding for investors looking to model financial scenarios. We’ll delve into the methodologies and tools that enable accurate predictions and analysis, crucial for strategic investment planning.
Please note that this analysis is conducted for educational and informational purposes only. It is not intended as financial advice, and no investment recommendations are made. The information presented in this study is based on historical data and experimental analyses, and does not guarantee future performance of Bitcoin or any other financial asset. Readers are encouraged to consult qualified finance and investment professionals before making investment decisions. The author and contributors disclaim all liability for decisions made based on the information provided in this article.
Much of the content in this article is inspired by a comprehensive training program I attended (Investment Management with Python and Machine Learning Specialization by EDHEC Business School) which focused on the concepts discussed herein.
Using the CIR Model to Simulate Zero Coupon Bond Yields and Prices
The Cox-Ingersoll-Ross (CIR) model is essential for simulating interest rate and predicting prices of zero coupon bonds within our portfolio. These bonds, which are acquired at a price lower than their nominal value and repaid at this same value at maturity. By integrating the CIR model, we can better adjust our allocation strategies between the growth and hedging portfolio, thereby optimizing investment returns while controlling risks associated with market rate fluctuations.
CIR Model Formula and example values (a stochastic differential equation) :
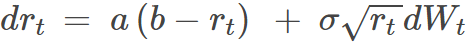
- drt is the infinitesimal change in the interest rate at time t.
- rt represents the instantaneous interest rate at time t = 0.03.
- a is the speed of mean reversion coefficient = 0.05.
- b is long-term mean level of interest rates = 0.03.
- σ is the volatility coefficient = 0.05.
- sqrt(rt) is the inclusion of the square root of rt in the volatility term ensures that volatility decreases when the interest rate is low, which helps prevent the simulation of negative interest rates.
- dWt represents an increment of a standard Brownian motion (or Wiener process), which models the random component of the rate change.
The result of the simulated interest rates for 10-year bonds and after 5000 scenarios :
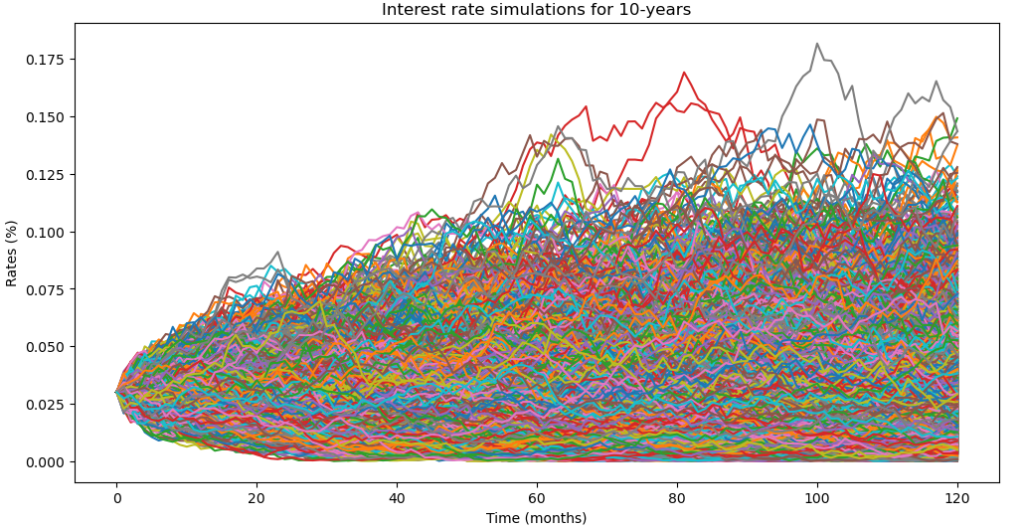
To simulate the price of the 10-year bonds using the simulated rates, we use the following formula :
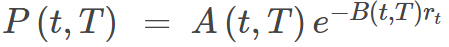
The result of the simulated zero-coupon bond prices for 10-year bonds and after 5000 scenarios :
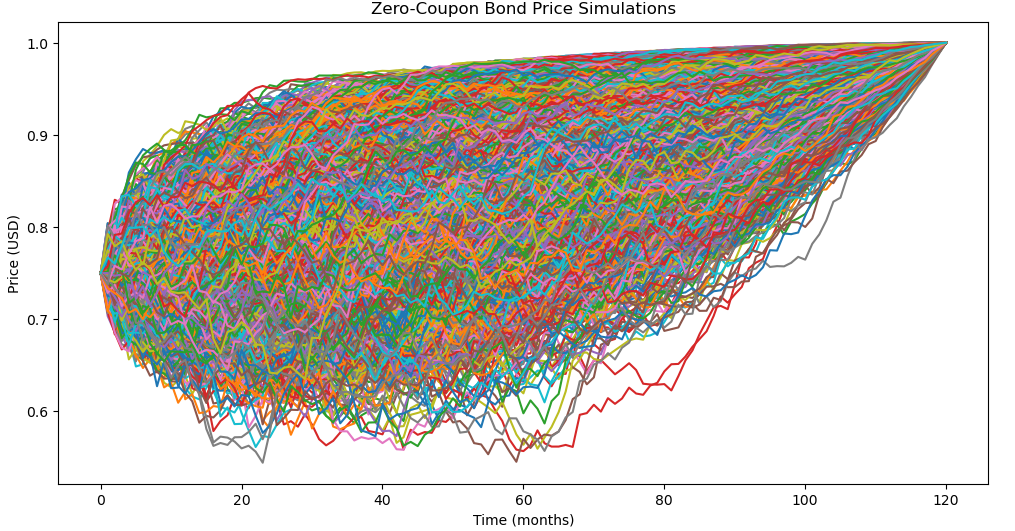
In simulating interest rates, it is crucial to note that, despite fluctuations, the face value of a bond is always repaid at maturity. This ensures that, regardless of market fluctuations, zero coupon bond holders will receive the promised face value, providing fundamental predictability and security to the investment.
Using the GBM Model to Simulate Equity Prices
Geometric Brownian Motion (GBM) is a statistical method commonly used in finance to model the dynamics of stock prices and other financial assets. It is a type of stochastic process that combines the elements of growth trends and random fluctuations.
GBM Model Formula and example values (a stochastic differential equation) :
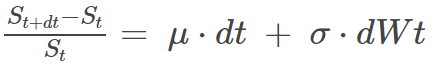
- dt is the infinitesimal change in time t.
- μ is the drift term representing the expected return of the asset per unit of time = 0.07.
- σ is the volatility coefficient = 0.15.
- dWt represents an increment of a standard Brownian motion (or Wiener process), which models the random component of the rate change.
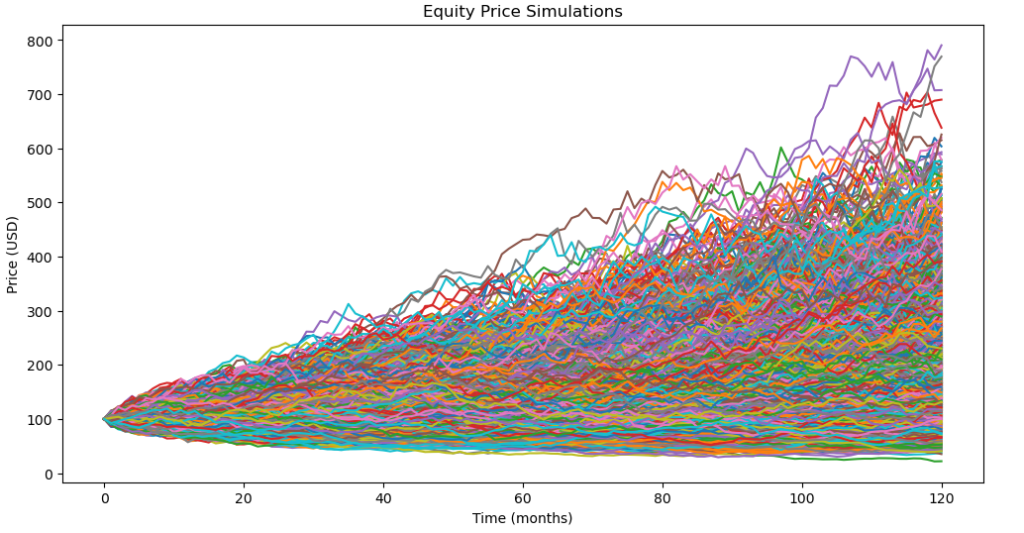
The result of the simulated equity prices for 5000 scenarios and $100 initially invested :
Conclusion
As we’ve explored throughout this article, effectively generating returns from bonds and accurately pricing equity are crucial skills for any investor. By understanding the underlying factors that influence bond yields and equity prices, investors can make informed decisions that align with their financial goals. This article has provided strategic insights into the mechanics of financial markets and investment tactics.

Laisser un commentaire